通过认真写好教案，我们可以更好地与学生进行互动，提高教学的参与性和趣味性，优秀教案的实施需要教师具备良好的组织和管理能力，心得范文网小编今天就为您带来了剪对称图形教案6篇，相信一定会对你有所帮助。

剪对称图形教案篇1

课题：1.1～1.4复习（初二上数学）b版

课型：复习

学习目标（学习重点）：

1、了解轴对称与轴对称图形，会准确画出轴对称 图形，找出对称轴、对称点等、

2、能熟练应用轴对称的性质、

3、复习线段的垂直平分线，角平分线的性质及推论，并能加以灵活运用、

例题：

例1、（1）下列说法中，正确的个数是（ ）

①轴对 称图形只有一条对称轴，②轴对称图形的对称轴是一条线段，③两个图形成轴对称，这两个图形是全等图形，④全等的两个图形一定成轴对称，⑤轴对称图形是指一个图形，而轴对称是指两个图形而言、

a、1个 b、2个 c、3个 d、4个

（2）如图在一个规格为6 ×12（即6×12个小正方形）的球台上，有两个小球 a，b。若击打小球a，经过球台边的反弹后，恰好击中小球b，那么小球a击出时，应瞄准球台边上的点（ ）

a、p1 b、p2 c、p3 d、p4

例2、作图题（1）作 出图1中△abc关于直线l的对称图形；

（2）如图2，∠bac＝60°，点p在边ac上，试用带刻度的直尺和量角器，在∠bac内部找一点o，使点o到a、p的距离相等，且到∠bac的两边的距离相等、

图1 图2

例3、已知：如图，△abc中，△abc的外角平分线ad，交bc的垂直平分线于d点，de⊥ab于点e，df⊥ac于点f，

（1）求证：be=cf；

（2 ）若ab=15，ac=7，求ae的长、

课后续助：

1、点a和点b关于直线l对称 ，对直线l任意一点p，必有pa____pb

2、对称图形________有一条对称轴，________有两条对称轴，_____ ___有四条对 称轴，_______有无数条对称轴。（各填上一个图形即可） 、

3、到三角形的三个顶点的距离相等的点是___________的交点、到三角形的三边的距离相等的点是___________的交点、

4、如果△ a bc与△a/b/c/关于直线l对称，且∠a＝500，∠b/＝700，那么

∠c/ ＝___ _、

5。如图，点p在∠aob内，pm⊥oa于m，pn⊥ob于n，且pm＝pn，连结op，则op是________________、依据是_______________ ________________、

6、如图，ab＝ac，ac的垂直平分线交bc于d，垂足为e，

若ab＝10，△abd的周长为23，求△abc的周长、

7、如图，有一个三角形纸片abc，ab=10cm，bc=7cm，ac=6cm，沿过点b的直线折叠这个三角形 ，使顶点c落在ab边上的点e处，折痕为bd，求△aed的周长、

8、如图，在△abc中，∠bac＝90°，be平分∠abc，de⊥bc于d，de=dc、

求证：bc＝ab＋ae、

9、如图，在四边形abcd中，bc＞ba，ad=cd，

bd平分∠abc，试说明：∠a+∠c=180°、

剪对称图形教案篇2

（一）创设情境，感知对称

本课的引入，课件展示一组美丽的轴对称图形，提出问题：这三幅图片有什么共同的特征？唤醒学生对轴对称图形的原有认识，引导学生回忆轴对称图形的概念，并板书关键词：对折完全重合

并揭题：图形的对称

这里多媒体演示的精美图片配以逼真的声效，是传统教学形式所达不到的，教学效果的区别也是很明显的。

（二）引导探索，研究对称

这部分我分为两个层次来教学：

1、探索长方形对称轴，指导学生画对称轴。首先第一部分探索长方形的对称轴，学生通过折一折并得出结论：长方形有2条对称轴，可以上下对折，也可以左右对折。并向学生介绍，这样的折痕在轴对称图形中是特有的，被称为对称轴。（板书：对称轴）。在学生交流的时候，教师同时课件演示折法，这样的演示，节省了大量的时间，让学生直观地感受到了长方形的两条对称轴的位置。

我把教学的重点放在了第二层次指导学生画对称轴上。教师在展示台示范用点划线画一条对称轴。并让学画对称轴。要求把另外一条也画出来。生自折自画自悟。教师深入，要是长方形在方格纸上，你还能找到别的方法画对称轴吗？（生说，师课件演示在格子图上数格子。）

教师继续深入，如果没有折痕，你能画出长方形的对称轴吗？在小组内讨论，得出取对边中点连线的方法。在交流时，课件出示用4把直尺测量找出长方形长和宽的中点，以此画出对称轴。

2、探索正方形的对称轴。

在第二层次探索正方形的对称轴过程中，我先让学生自己动手折一折，操作验证，再在书上画出结果。

展示的时候，先交流画2条对称轴的图形。

然后展示画4条对称轴的图形补充，指着两条对角线所在的对称轴，提问：为什么正方形的对角线是它的对称轴，而长方形的对角线却不是对称轴呢？

根据学生回答，教师展示课件正方形4种对折方法的动态演示。

师总结：正因为如此，正方形有4条对称轴，而长方形只有2条对称轴。（板书）

（三）探究提高，巩固对称

练习部分，我比较注重对习题的开发和利用，进行适当地顺序调整，拓展和延伸，使练习部分成为本课的亮点。主要分为3个层次来练习。

1、基础练习（想想做做第1题）

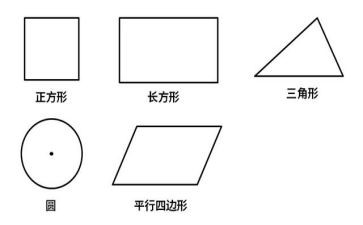
请同学们拿出6个图形，折一折，判断哪些是轴对称图形，哪些不是。是轴对称图形的，画出它的对称轴。接着学生在交流时可以使用展示平台，学生可以完全看清操作过程。

这一题是对基础知识的巩固。

2、提高练习（想想做做第4题）

题目要求学生先画出正三角形、正方形、正五边形、正六边形的对称轴，学生独立完成后，集体交流。

根据部分学生的答案，课件填表格。我适当追问，引起学生思考：按照这样推断，那正七边形会有几条对称轴？正十边形呢？正一百边形呢？

让学生归纳总结出规律：正多边形，对称轴的条数与边数相等。

3、综合练习

①比较复杂图案的对称轴。（想想做做第2题）

出示4个复杂图形，学生独立完成，再集体交流。（根据学生回答，课件演示对称轴）

②根据对称轴所在的位置，画出轴对称图形的另一半。（想想做做第3题）

学生独立完成，交流时让学生说说怎样找关键点最准确。配合课件和学生的回答，动态演示先找到对应的关键点，然后将这几个点相连。

（四）总结反思，升华对称

首先让学生说说你有什么新的收获。

其次学生说说生活中的对称现象。

（五）创新设计，运用对称

请学生发挥自己的聪明才智，在方格纸上设计一个美丽的轴对称图形（课件出示方格纸）。

剪对称图形教案篇3

教学内容

教科书第100～101页，练习二十六的第1～6题．

教学目的

使学生初步认识轴对称图形，知道轴对称的含义，能够找出轴对称图形的对称轴．

教具、学具准备

教师准备一些实物图、剪纸、剪刀，学生准备剪刀、方格作图纸、直尺．

教学过程

一、新课

1．教学轴对称图形．

教师出示教科书第100页上面的实物图和一些轴对称的剪纸，让学生观察它们有什么特点．使学生初步体会到这些实物图有“轴对称”的特点．

然后教师和学生仿照教科书第100页中间的`图形用纸剪一剪，让学生观察、讨论剪完的图形有什么特征．

教师指出：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形；折痕所在的这条直线叫做对称轴．

2．做教科书第100页下面的“做一做”的题目．

让学生通过观察进行判断，教师还可以再出示一些图形让学生观察．

3．教学轴对称的几何图形．

教师让学生拿出方格纸，按照教科书第101页上面的图画出这些图形，再剪下来折一折，判断这些图形是不是轴对称图形，并画出它们的对称轴．然后让学生观察在一个图形中有没有不止一条对称轴的．

再让学生把轴对称图形和非轴对称图形进行比较，比如把等腰三角形和它左边的锐角三角形进行比较，使学生认识到等腰三角形是轴对称图形，它的两条腰两个底角分别相等；而它右边的这个锐角三角形就没有这些特性，不是轴对称图形．

4．做教科书第101页“做一做”中的题目．

让学生根据轴对称图形的概念进行判断，并画出对称轴，还可以让学生简单地说一说自己判断的理由．

5．教学轴对称图形的性质．

教师让学生拿出直尺，量一量第101页“做一做”中每个轴对称图形左右两侧相对的点到对称轴的距离，能不能发现什么规律．

教师小结：在轴对称图形中，对称轴两侧相对的点到对称轴的距离相等．

二、课堂练习

做练习五的第1～6题．

1．第1题，让学生说一说自己是怎样判断的，尤其是第4个图，多让几个学生说一说．

2．第2题，要让学生找出教科书上没有出现过的三个轴对称图形．比如说红领巾、量角器、黑板、桌面、电视机等等．

3．第3题，让每个学生都动手剪一剪，再说一说剪下的图形展开后，是不是轴对称图形，使学生知道对称性质在服装等行业中的用处，进而认识到对称性质的用途是十分广泛的．

4．第4题，让学生仔细观察、判断，再找出“0”、“8”各有几条对称轴．

5．第5题，先让学生回忆学过哪些平面图形，再找出哪些是轴对称图形，各有几条对称轴．

6．第6题，指名到前面画，观察学生第1个图怎样画对称轴，第2个图画几条对称轴．

剪对称图形教案篇4

【教学内容】

人教版义务教育课程标准实验教科书二年级上册p68。

【教学目标】

1、了解生活中的对称现象，认识轴对称图形的一正些基本特征。能正确识别轴对称图形，会设计制作简单的轴对称图形。

2、通过观察、猜想、验证、操作，经历认识轴对称图形的过程，掌握判断轴对称图形的方法，培养学生的动手、创新能力。

3、在认识、制作和欣赏轴对称图形的过程中感受物体或图形的对称美。

【教学重点】

认识轴对称图形的基本特征。

【教学难点】

设计制作轴对称图形。

【教具、学具准备】

教师准备课件、一个蝴蝶图形；学生彩纸、剪刀、直尺及若干对称图形和不对称图形。

【教学过程】

一、创设情境，感受对称

1、认识生活中的对称现象。眼镜导入新课。

二、小组合作，探讨轴对称图形的特征

1、认识对称图形

师：看，老师还给大家带来了几张美丽的图片。

生：蜻蜓、树叶、蝴蝶、脸谱的图片

师：请孩子们仔细观察这些图形，你能发现它们共同的特征吗?

生1：它们的两边一样的。

生2：它们是对称的。

师：你是怎样理解对称的？

生2：它们的两边是一样的。

师：这些图形真像你们说的那样，左右两边完全一样吗？

生：是。

师：谁能想个办法来验证这些图形左右两边完全一样呢？

生：对折。

师：对折，这个方法听起来倒挺不错的，（板书：对折）到底怎样对折，你能折给大家看一看吗？

生：上台演示折蝴蝶图形

师：刚才这位孩子用对折的'方法证明了这个蝴蝶图形的左右两边是完全一样的。那大家也来试一试，好吗？

生齐：好。

师：那先听清楚要求：请小组长拿出1号信封里的4张图片，小组里的每个同学，把其中一个图形对折一下，看看这些图形的两边是一样的吗？开始吧。

生：动手操作

师：谁来说说你验证的结果？

生1：我折的是脸谱图形，对折后它的两边是一样的。

生2：我折的是蜻蜓图形，它对折后，两边是一样的。

生3：我折的是蝴蝶图形，对折后它的两边是完全一样的。

生4：我折的是树叶图形，对折后，它的两边也是完全一样的。

师：孩子们刚才折这些图形，对折后，它们的两边都是完全一样的，我们就说它们对折后，它们的两边重合了。

师：老师这里还有一个图形，是什么？

生：桃子图形。

师：想折吗？

生齐：想。

师：这个图形就在你们的3号信封里，小组长拿出来分给同学们折一折，说说你发现了什么？

生1：我发现了桃子图形一边大，一边小。

生2：它没有重合。

师：一点都没有吗？

生齐：有一点。

师：蝴蝶图形呢？

生齐：全部重合了。

师：像蝴蝶图形这样对折后两边全部重合我们就称为完全重合。

师：孩子们看大屏幕（课件演示蜻蜓、树叶、蝴蝶、脸谱四个图形对折后左右两完全重合的画面）

教师小结：像这样对折后，两边完全重合的图形，我们就把它叫做“对称图形”。（板书：对称）

2、认识对称轴

师：请大家打开对折后的对称图形，看一看，你又有什么新的发现？（把图贴在黑板上）

生：有一条线。

师：这一条线就是我们刚才折的折痕。

师：这条折痕是怎么形成的？有什么特别的地方?

生1：是对称图形对折后形成的。

生2：折痕的两边是完全一样的。

师：这样的折痕是对称图形中特有的，所以人们把这条折痕所在位置的直线，给它起了个形象简洁的名字，叫对称轴。（板书：对称轴）

师：我们通常用虚线来表示对称轴。（板书：画对称轴）

师：像这样，对折后，对称轴两边完全重合的图形我们就叫做“轴对称图形”。 (板书：轴)

三、应用拓展、巩固新知

1、判断轴对称图形

师：刚才我们认识了轴对称图形，那给你一些图形，你能找出轴对称图形吗？（课件出示：p68的做一做）

2、猜一猜

师：老师给你们看几张轴对称图形，不过我只给你们看它的一半，你们能猜出它们是我们所学过的哪些汉字、数字或英文字母吗？

3、找对称轴

师：今天，老师还给你们带来了几个图形老朋友，打个招呼吧！

（课件依次出示：长方形、正方形、圆形）

师：这几个图形各有几条对称轴呢，请你折一折。（边说边点课件出示）

四、师生共结

师：孩子们真会观察生活，对称的物体真是无处不在，只要孩子们留心观察，我相信你们还会找到更多更美的对称。

剪对称图形教案篇5

教学目标：

1、低层目标：让每个学生都知道什么样的图形是对称图形，并能找出它的一条对称轴。

2、高层目标：使学生能根据不同的对称图形找出不同的对称轴，并会设计制作对称图形。

3、发展目标：通过学习，发展学生的空间观念，培养学生的观察能力、动手操作能力以及欣赏数学美的意识。

教学重难点：

能准确判断对称图形，会找对称轴。

教学准备：

课件、对称图片、彩纸、剪刀。

教学过程：

一、情境引入

师：刚才大家已经看了这么多的图片，现在你有什么想说的吗？

学生讲自己的想法。

师：同学们都说出了自己的想法，有些同学认为它们很美，有些认为它们色彩漂亮，还有的同学发现了它们这些图形的两边都是一样的。同学们说得都很好，下面我们就来着重地研究一下，这些图形是不是象**同学所说得那样，它们的两边都是一样的。（边说边演示课件，让学生感知左右或上下一样）

二、认识轴对称图形

1、认识轴对称图形的特征。

师：刚才我们用肉眼观察到这几个图形的左右两面和上下两面都是一样的，象这样的学习方法我们通常把它叫做观察法。（板书：观察法）

师：那么，除了观察法你还有什么方法可以来证明它们两边肯定一样吗？（根据学生回答板书：如：测量法）当学生提出对折时，就拿出准备好的树叶图片：你看老师就准备了一片树叶，你准备怎样对折？（请学生上来对折）对折后，你们发现怎么了？（重叠了）数学上把这种现象叫完全重合（板书：完全重合）那么完全重合了，也意味着它们左右两边完全一样。通过对折证明了树叶的左右两边一样，我们就把这种方法称为对折法。（板书：对折法）

下面我们就用对折法来看看剩下的图形是不是如我们观察到的两边一模一样。（课件演示）

小结：刚才这些图形我们通过观察法和对折法都发现了它们两边左右两边或上下两面一样，用对折法发现它们对折后能完全重合，像这样的图形就是我们今天要学习的对称图形（板书课题）。

2、认识对称轴。

师：朱老师也剪了几个图形，想让你们猜一猜我剪的是什么，并判断一下它是对称图形吗。（出示一半的：青蛙、飞机、爱心、衣服）

以上图形一个一个出示，当出现衣服时，问学生为什么这个不是对称图形？为什么？

师：那我们就来看这3个对称图形，你们有没有发现它们图中都有一条折痕，你们看这条折痕刚好把这个图形怎么样了？（分成了两边一样的部分）这条折痕是一条什么线？你能给这条重要的线取个名字吗？（学生说）我们数学上把这条折痕称为“对称轴”，人们一般用虚线来画对称轴。（选一个图形画出对称轴），那么象这个图形，它不是对称图形，它能画出对称轴吗？为什么？

三、应用

书上也有一些图形，请大家把书翻到第68页，请小朋友们仔细看看，是不是对称图形，如果是请画出对称轴。

学生做，教师巡视，请学生上来汇报。（当学生对五角星争议时，拿出做好的五角星，让学生上来折一折，教师画出对称轴。）

小结：说明有些图形的对称轴不止一条，它可以是左右对称，上下对称或斜着对称。其它题目要指出画对称轴要画准，两边要一样，这可利用同桌检查的方法。

师：刚才大家都认为“1”不是对称图形，这是为什么呢？0～9这10个数字里你觉得哪几个数字是对称的？（0、8、3）

四、找一找：其实生活中还有很多东西也是对称的？你能举一些吗？（学生举例）

是啊，我们生活中的对称现象真是太多了。

五、巩固深化

你看，朱老师我也带来了一些图形（出示：长方形、正方形、圆），它们是对称图形吗？能找出对称轴吗？下面我们就根据这三个图形来个比赛，比赛的题目是“比比谁的眼力准”，请大家拿出练习纸先看练习的第一题（教师介绍：我们先猜想正方形的对称轴有几条，把数字填进去，再通过实际操作验证是否正确，得出准确的条数，如果你的验证与猜想一致，你就在评价栏中涂上一颗红星，如果比较接近则涂上一颗黄星，如果都错了就不涂，明白了吗？）

师：下面，请每位同学到四人小组组长地方拿一个正方形，先请你看着正方形猜想一下它的对称轴有几条，然后把猜好的数填在表格中，现在你动手折一折或画一画，看看它到底有几条对称轴，学生折完后，请一生上来展示，得出正方形有4条对称轴，然后涂五角星进行评价。（折长方形、圆方法同上）

得出长方形只有两条对称轴，圆有无数条对称轴。

小结：通过刚才我们动手折一折，画一画，我们知道原来不同的对称图形，对称轴的条数也不同，有的只有1条，有的有两条，有的甚至有无数条。

六、创造对称图形

师：大家已经认识了对称图形，知道了对称轴，也体会了生活中对称图形的美，现在想不想动手来创造一些对称图形呢？请大家拿出老师发给你的彩色纸请小组讨论一下用什么方法来剪，剪出的肯定是对称图形。（小组讨论后汇报）教师指出：大家剪的过程中如果有什么困难可以向其他同学请教。剪完后，可以把自己的作品贴在黑板上。（学生剪，并在黑板上贴出）

七、小结

1、今天这节课你学得开心吗？为什么？

2、如果用笑脸来评价自己的话，你认为今天你可以得到几张笑脸？为什么？

3、想不想知道老师今天对大家这节课表现的评价？我认为今天大家表现都很棒，所以老师送给你们5张笑脸。（出示课件）

4、你们再仔细瞧瞧，其实这5张笑脸组成的一个图形也是对称图形，它的对称轴在哪呢？（学生争论后课件出示对称轴）那如果有10张笑脸呢？（学生课后讨论）

剪对称图形教案篇6

第四单元

第五课时：轴对称图形

教学内容：轴对称图形、对称轴、对称性质；课本第100～101页，完成相应的“做一做”题目和练习二十六的第1～7题。

教学目的：使学生初步认识轴对称图形与对称轴；会找出对称图形的对称轴；并知道对称轴两侧相对的点到对称轴的距离相等。

教具、学具：剪刀、复写纸、白纸。

教学过程：

一、复习。

说一说你是如何用对折的方法找出一个圆的圆心的。

二、新授。

1．导入。

在日常生活中，我们会看到一些物体或图形很特别，把它们像圆一样沿着一条线对折，两边就完全重合；如枫树叶、蝴蝶（出示图形）等这些图有对称美；那么，到底什么样的图形才是轴对称图形，这就是我们今天要学的内容。

板书课题：轴对称图形。

2．轴对称图形与对称轴。

教师把一张白纸对折，中间夹上双面复写纸，在纸上面画半个花瓶，然后把纸展开，得到以折痕为对称轴的整个花瓶。

从图中不难发现折痕两侧物体形状与图形的大小完全一样。

师生一起打开课本第121页，看上半页的三个图（树叶、蜻蜓、天平）由学生说一说他们的特点。（他们以树叶的主干、蜻蜓的身躯、天平的指针为轴左右两侧形状、大小一样。）

做课本上的`实验，把一张纸对折并按书中的图样画好，再用剪刀剪下，把纸打开可看到它是以树干这直线为轴，两侧的图形能够完全重合。

小结：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形（指着树叶等）就是轴对称图形。折痕所在的这条直线叫做对称轴。

回答课本第121页下面的“做一做”。

3．画（找对称轴）。

对称轴的轴法是一横一点一横点穿过图形，如“—·—·—”。先要求学生判断下面图形是否轴对称图形？然后要求学生判断下面图形是否轴对称图形？

学生画出对称轴。

最后要求学生在课本上量一量对称轴两侧相对的点到对称轴的距离是否相等。通过多处的测量可概括出：在轴对称图形中，对称轴两侧相对的点到对称轴的距离相等。

三、巩固练习。

1．课本100页“做一做”第1题。

第四单元

2．课本第101页“做一做”第2题。先找出对称轴然后再量一量对称轴两侧

相对的点距离是否相等。

3．练习二十六第1～6题。

课后小结：

读书破万卷下笔如有神，以上就是一秘为大家带来的6篇《《轴对称图形》教案》，希望可以对您的写作有一定的参考作用，更多精彩的范文样本、模板格式尽在一秘。